eBTC Retrospective

A reflection on lessons learned in our extended fuzzing of eBTC

In our second engagement with the eBTC protocol the Recon team increased fork testing coverage of their system and added coverage of the yield distribution mechanism which we call the Yield Story.

Note: this retrospective is also available in video form here.

eBTC

To understand eBTC from a high level we turn to the description provided by Antonio in the lessons learned from the first engagement:

eBTC is a collateralized crypto asset soft pegged to the price of Bitcoin and built on the Ethereum network. It is backed exclusively by Lido Staked ETH (stETH), and built on top of Liquity's LUSD model to maintain its peg stability. Users create Collateralized Debt Positions (CDP) by depositing stETH into the protocol, which allows them to mint eBTC, that can later be used in DeFi and redeemed back for stETH.

Takeaways

In our first engagement with eBTC some forked integration testing had been performed but there were gaps left in coverage due to time constraints which were addressed in this second engagement.

With the full eBTC system being deployed during this engagement, we were able to conduct end-to-end fork testing but this introduced challenges related to initial decreases in coverage that were handled using the methods described in the takeaways below.

1. Be wary of mocks

In the first phase of the forked fuzzing engagement only the dependency contracts used their mainnet deployment implementations in the system setup. This allowed minimal reconfiguration of the test suite that had been developed for local testing.

However, since mocks had initially been used to wrap some of these integrating contracts with a simpler interface for manipulating their state values, when they were replaced with their actual implementation contracts some differences between the mock interface and implementation interface introduced unexpected behavior.

In the pre-forked fuzzing suite, the team had implemented a mock of the stETH collateral token StETHMock which had the following submit function defined on it:

function submit(uint256 _sharesAmount) external {
        _mintShares(msg.sender, _sharesAmount);
}

However, the actual deployed stETH contract on mainnet has the following implementation of the submit function:

function submit(address _referral) external payable returns (uint256) {
        return _submit(_referral);
}

The resulting difference in the function signatures meant that calls to the function when wrapped with the mock interface that had previously been used would silently revert. This ultimately resulted in coverage in fork testing being lower than in the local testing setup.

To avoid such errors, it’s recommended to perform a differential fuzz between the mock and the implementation contract, this can help increase confidence that the mock being used is congruent with the actual implementation.

2. Work with what you have

In the full end-to-end forked fuzzing phase of the engagement the team focused on ensuring the existing fuzzing suite was able to still achieve the same coverage as the local and semi-forked suite.

One of the key components of the fuzzing suite was allowing the fuzzer to simulate on-chain actions outside of the eBTC system which have side effects on the system’s behavior, which creates a more realistic simulation of how the system state may evolve.

In our case eBTC integrates with Lido’s stETH as part of its yield accrual mechanism. Since stETH is a rebasing token it’s therefore subject to variations in supply, where holder’s shares increase as staking rewards are earned and decreases in the event of a slashing penalty. The effect of this change in stETH supply on the eBTC system is fundamentally a change in the exchange rate between stETH/eBTC, determined by the price provided by an oracle used in the eBTC system.

We therefore wanted to allow the fuzzer to manipulate the price returned by the oracle in a way that realistically simulates a rebasing event, so the team implemented a function which when called by the fuzzer directly manipulates the values returned by the oracle to achieve the same effect of a rebase event which would manipulate the quantity of stETH.

The easiest way to do this was by manipulating the oracle contract’s storage slot which held the state variable value corresponding to the price, using the HEVM store cheatcode:

function setPrice(uint256 newPrice) public override {
        _before(bytes32(0));

        // Sets the current price to zero to trigger the oracle fallback to the last good price
        hevm.store(
            address(priceFeedMock),
            0x0000000000000000000000000000000000000000000000000000000000000002,
            bytes32(0)
        );


        // Load last good price
        uint256 oldPrice = uint256(
            hevm.load(
                address(priceFeedMock),
                0x0000000000000000000000000000000000000000000000000000000000000001
            )
        );
        // Calculates new price
        newPrice = between(
            newPrice,
            (oldPrice * 1e18) / MAX_PRICE_CHANGE_PERCENT,
            (oldPrice * MAX_PRICE_CHANGE_PERCENT) / 1e18
        );


        // Set new price by etching last good price
        hevm.store(
            address(priceFeedMock),
            0x0000000000000000000000000000000000000000000000000000000000000001,
            bytes32(newPrice)
        );


        cdpManager.syncGlobalAccountingAndGracePeriod();


        _after(bytes32(0));
    }

Using the previous price for calculating the new price ensured the fuzzer didn’t introduce false positives by using unrealistic price changes that wouldn’t actually occur in practice during an actual rebase event.

Ultimately this allowed the team to achieve the same degree of coverage as with local testing and run fork tests against the continuously evolving mainnet chain state (Recon also offers this as a service).

3. Prove by induction where possible

After the above fork testing of the core functionality was concluded and shown to behave as expected, the team moved on to testing properties related to eBTC’s yield distribution mechanism which we called the Yield Story.

eBTC distributes yield via a profit-yield-sharing mechanism in which a fraction of yield earned by the stETH in the system during a rebase event is sent to the protocol as a fee and the remainder distributed to protocol participants. The profit yield sharing (PYS) formula achieves this using user shares to calculate how much each is owed and how much to deduct from each user.

Our objective as part of the yield story therefore was to prove that this formula is in fact correct, without simply replicating it’s implementation in the invariant that’s supposed to prove it. The corresponding implementation in the invariant therefore used percentages instead of shares to calculate the yield distribution in a manner that was congruent to the protocol implementation and allowed comparing the resultant yield calculations for equality.

// As a protocol, we expect the yield growth from moment to moment to be equal to the PYS, given a positive yield 
    function invariant_PYS_04(CdpManager cdpManager, Vars memory vars) internal view returns (bool) {
        ...

        if (vars.yieldStEthIndexAfter > vars.yieldStEthIndexBefore) {
            uint256 yieldGrowthPercent = (vars.yieldStEthIndexAfter - vars.yieldStEthIndexBefore) * 1e18 / vars.yieldStEthIndexBefore;
            // The protocol's claimable fees should increase by the PYS % on the expected increase of the system collateral shares value
            uint256 feesTakenExpected = (vars.yieldProtocolValueBefore * yieldGrowthPercent / 1e18)
                * cdpManager.stakingRewardSplit() / cdpManager.MAX_REWARD_SPLIT();

            uint256 feesTakenActual = vars.feeRecipientCollSharesAfter - vars.feeRecipientCollSharesBefore;

            require((vars.yieldProtocolCollSharesBefore - vars.yieldProtocolCollSharesAfter) == feesTakenActual, "!fees taken should be synced");

            feesTakenExpected = collateral.getSharesByPooledEth(feesTakenExpected);
            collateral.getSharesByPooledEth(feesTakenActual);

            return _assertApproximateEq(feesTakenExpected, feesTakenActual, 1e6);
        }
      ... 
    }

In addition, since the yield would be updated by any function that syncs the yield growth, there is no good way to test that for an arbitrary amount of time between calls to sync yield growth that the yield is accumulated correctly. Instead, using the fact that the yield accumulates as a result of rebasing events by stETH, we check that for each rebasing event the yield is properly accumulated.

The mechanic implemented is described by the following graphs:

We proved that the yield growth in the system within individual rebase events was the same as the yield growth expected by the PYS formula over any given time period.

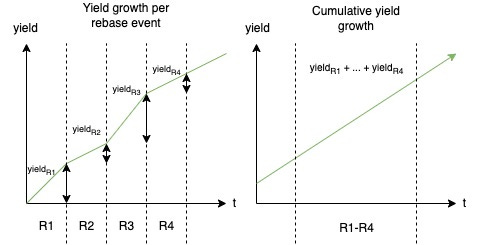
This was implemented in invariant_PYS_04 which checks that for each rebase event, the yield growth is equal to the expected value returned by the PYS formula.

This makes use of the fact that in order to prove some property, instead of trying to prove the final result (the overall yield delta), if we can prove that for each individual event that contributes to the yield delta that the property holds, then we can state that the cumulative result also holds by induction. This is much simpler not only in implementation but also because it requires fewer test cases and allows us to know the behavior of the system is the same for several rebase events as it is for infinitely many.

Conclusion

Forked fuzz testing offers a greater resolution to protocol behavior but can introduce its own complexities into a testing suite.

Care should be taken to adapt the test suite where needed to ensure coverage is comparable to pre-fork testing levels.

There is no one way to accomplish this as was shown in the examples above and requires running the fuzzer to see what may actually be causing reductions in coverage.